第13周期的预测销售量为：

　　F 13=(500+508+480+600+600+660+590+700+680+740+790+760)÷12

　　这种方法是时间序列分析法的另一种极端情况，它考虑了时间序列的全部数据，但把它们都平均了。这种方法的特征是反映需求变化最慢，稳定性强，灵敏性小。算术平均数法适合稳定形态的预测，如用于趋势形态和季节性形态则误差较大。

　　这种方法是时间序列分析法的另一种极端情况，它考虑了时间序列的全部数据，但把它们都平均了。这种方法的特征是反映需求变化最慢，稳定性强，灵敏性小。算术平均数法适合稳定形态的预测，如用于趋势形态和季节性形态则误差较大。

　　(3)移动平均数法：包括一次移动平均数法和二次移动平均数法。

　　1)一次移动平均数法：即用过去m个周期实际销售量的算术平均值作为下期销售量的预测值。这种方法只选取了时间序列中最靠近预测期的一组数据，选取的数据个数(m)固定不变，而随着预测期向前移动，每组数据的观察期也向前移动。公式：

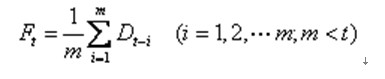
　　式中：Ft——第t期的预测销售量;

　　Dt-i——第t-i期的实际销售量;

　　m——移动平均所取实际销售量的期数，简称为移动期数。

 【例2】某商品流通企业某种商品1—12周期的实际销售量如表4—2所示。如取m=3，则移动平均数法的各周期预测值F如表4—2所示。用一次移动平均书法求第13周期的销售量预测值。

　　由于移动期数m为3，故从第4周期起才开始运算：

　　一次移动平均法是介于上期销售量法和算术平均法之间的一种方法。

　　2)二次移动平均数法

　　二次移动平均数法是利用预测目标时间序列的一次移动平均值和二次移动平均值的滞后偏差演变规律建立起线性方程进行预测的方法。二次移动平均值是以一次移动平均值作为时间序列，再计算第二次的移动平均值，移动期数不变。二次移动平均数法的线性方程式为：

　　【例3】某商品流通企业某种商品1—12周期的实际销售量如表4—3所示。如取α=0.8，则指数平滑法的各周期预测值如表4—3所示。此表中的预测值均四舍五入为整数。

　　表4—3

　　假设第1期的预测值为500，然后代入公式，依次运算：

　　F 2=0.8×500+(1-0.8)×500=500(千克)

　　F 3=0.8×510+(1-0.8)×500=508(千克)

　　F 4=0.8×480+(1-0.8)×508=486(千克)

　　其余类推。如预测第13期的销售量，则

　　F 13=0.8×760+(1-0.8)×778=764(千克)

　　指数平滑法考虑了时间序列的全部数据，但对接近的数据给予较大的权数，对早期的数据给予递减的权数。平滑系数α越大，越接近1，对近期数据加的权数越大，反映需求变化的灵敏度越高;反之，α越小，对需求变化反映的灵敏度就越差。和移动平均数法m值的选取方法一样，指数平滑法α值的选取，可由预测者经验判断误差，也可用试验方法，先选用若干个α值对时间序列做实验，并比较不同α之的预测误差，选取误差较小单的α值用于预测。

[1] [2] [3]

　　考试交流区报名时间交流群（点击加入QQ群可快速加群交流成绩查询相关信息我们会及时在群里通知）：

　　（群：569977370）　

　　温馨提示：有任何报考及考试相关疑问，可添加网校专业老师个人微信号“edu24olxu”咨询。！考生可下载手机APP，随时掌握考试资讯！

扫一扫上面的二维码，添加老师个人微信号，所有课程八折开通