所谓相关分析,是研究现象之间是否存在某种依存关系,并对具体有依存关系的现象探讨其相关方向以及相关程度,是研究随机变量之间的相关关系的一种统计方法。
变量之间的相关关系主要有线性相关和非线性相关、正相关和负相关等几种形式。
对两个变量间线性相关程度的测量称为简单相关系数。样本相关系数定义公式为:
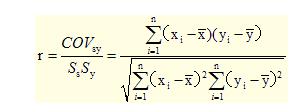
式中,r为样本相关系数,COVXY为协方差,Sx、Sy分别是变量x和y的标准差。(注意:公式中分子分母求和表达式中应该是i=1到n,而不是n=1到n)
相关系数r的取值范围在-1~+1之间。
·r=1或r=-1时,表明变量间的关系为完全正相关或完全负相关,这是两种极端的情况,实际上表明两个变量之间是线性关系;
·r=0时,表明变量间不存在线性相关关系,可能是无相关,也可能是非线性相关;
·0<r<1时,表明变量间存在正相关关系;
·-l<r<0时,表明变量同存在负相关关系。
|r|愈接近于l,变量间相关程度愈高,|r|愈接近于0,相关程度愈低。
在一般情况下,总体相关系数p是未知的,一般是用样本相关系数r作为总体相关系数P的估计值。但由于存在样本抽样的随机性,样本相关系数并不直接反映总体相关程度,因而,计算出来的样本相关系数在多大程度上值得信赖,需要进行检验。
|r|<自由度(df)为(n-2)的t统计量t(n-2)、显著性为a(10%;5%)的相关系数(查相关系数表),其相关性是显著的。所谓“显著水平”或r=0,指的是很少会发生的概率。

在实际中,因为研究目的、变量类型的不同,采用的相关分析也不同。比较常用的相关分析有二元定距变量的相关分析、二元定序变量的相关分析、偏相关分析和距离分析等。
(二)推论统计分析
推论统计是在随机抽样的基础上,根据部分资料(数据)推断总体的方法,也即利用样本资料对抽出样本的总体做出推论的方法。
1.单个样本的参数估计
参数是指总体的某一特征值,如均值、方差等,往往是未知数;而根据样本数据计算出来的均值、样本标准差、样本比例一般称为样本“统计量”。参数估计是根据样本统计量对总体未知参数进行某种估计推断。
(1)点估计。当总体分布的形式已知,但其中的一个或多个参数未知时,如果从总体中抽取一个样本,用该样本对未知参数作一个数值点的估计,称为参数的点估计。
例如:假设对北京1800万人的工资水平进行调查,一般情况下,需要进行抽样调查,假设抽取1000个样本,得出的平均工资为2500元每月,这个2500就是样本的平均值,用 来表示,方差为200,所谓的点估计就是直接用样本的均值和方差来表示总体的均值和方差,即北京1800万人的平均工资就是2500元,方差为200。
点估计有多种方法,如矩法、最大似然法、最小二乘法等。
考试交流区报名时间交流群(点击加入QQ群可快速加群交流成绩查询相关信息我们会及时在群里通知):
温馨提示:有任何报考及考试相关疑问,可添加网校专业老师个人微信号“edu24olxu”咨询。!考生可下载手机APP,随时掌握考试资讯!

扫一扫上面的二维码,添加老师个人微信号,所有课程八折开通
相关文章
如果本站所转载内容不慎侵犯了您的权益,请与我们联系
 ,我们将会及时处理。如转载本站内容,请注明来源:经济师考试网(jjsexam.COM)。
,我们将会及时处理。如转载本站内容,请注明来源:经济师考试网(jjsexam.COM)。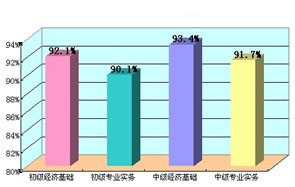
环球网校经济师历年通过率比较
 刘艳霞老师 |
刘艳霞老师:会计师、注册会计师。环球职业教育在线会计职称、注册税务师、注册会计师、会计从业、经济师等课程辅导专家。...[详细] |
 胡艳君老师 |
胡艳君老师,上海财经大学经济学博士。任职于北京某高校经济学类、管理学类的辅导老师。.[详细] |




